Assumptions of Linear Regression

Simple Linear Regression is when we consider a single independent variable. Whereas an examination of many independent variables is called multiple linear regression.

Linear Regression has 5 key assumptions:

• Linear relationship
• Multivariate normality
• No or little multicollinearity
• No auto-correlation
• Homoscedasticity

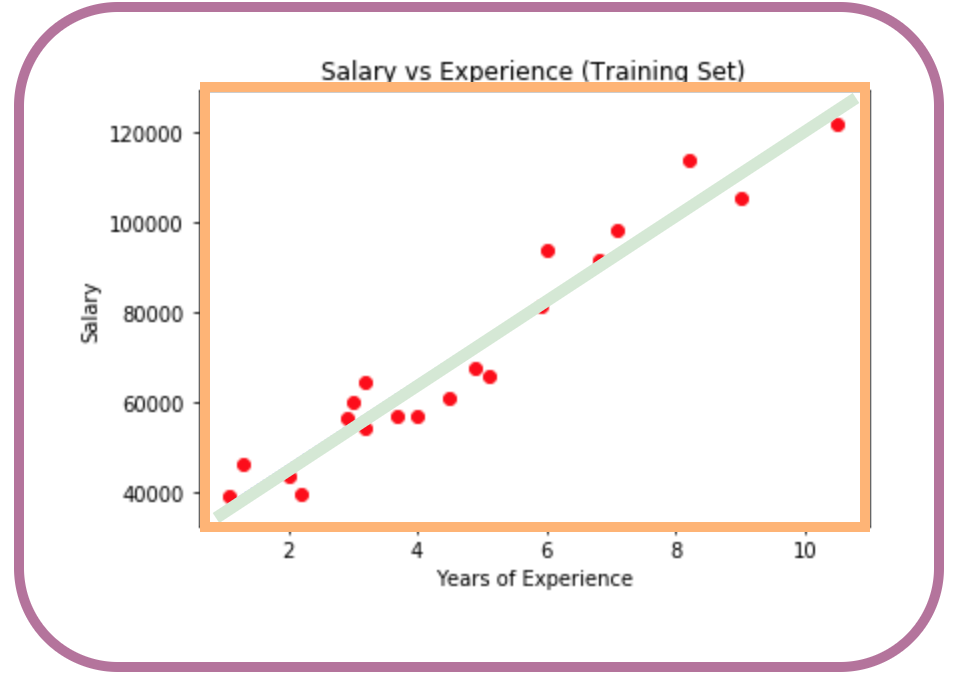
Linear relationship requires a relationship between the independent and the dependent variables to be linear. For example; Salary vs Experience typically has a good linear relationship, whereas Hair colour vs Height would have little, to no, linear relationship. If your data set is not obvious upfront, then a simple scatter plot can help you visualise this.

plot(x, y, main, xlab, ylab, xlim, ylim, axes)

Multivariate normality is to avoid a few out-liners skewing with the model. Normality can be tested with a Goodness of Fitness test such as the Kolmogorov-Smirnov test.

Multicollinearity occurs when the independent variables are too closely correlated with each other. The problem with multicollinearity is that one predictor variable can be predicted with high accuracy based on the other variables around it, the reason this is an issue we need to be aware of is that should a variable slightly deviate from this phenomenon then the regression model would be adversely affected as a result.

Auto-correlation occurs when the residuals are not independent from each other. For instance, this typically occurs in stock prices, where the price is not independent from the previous price.

Homoscedasticity means that residuals are similar across the group.

In statistics, a sequence or a vector of random variables is homoscedastic if all random variables in the sequence or vector have the same finite variance.